计算机组成2上-数据表示

2.1 数据表示

2.1.1 概述

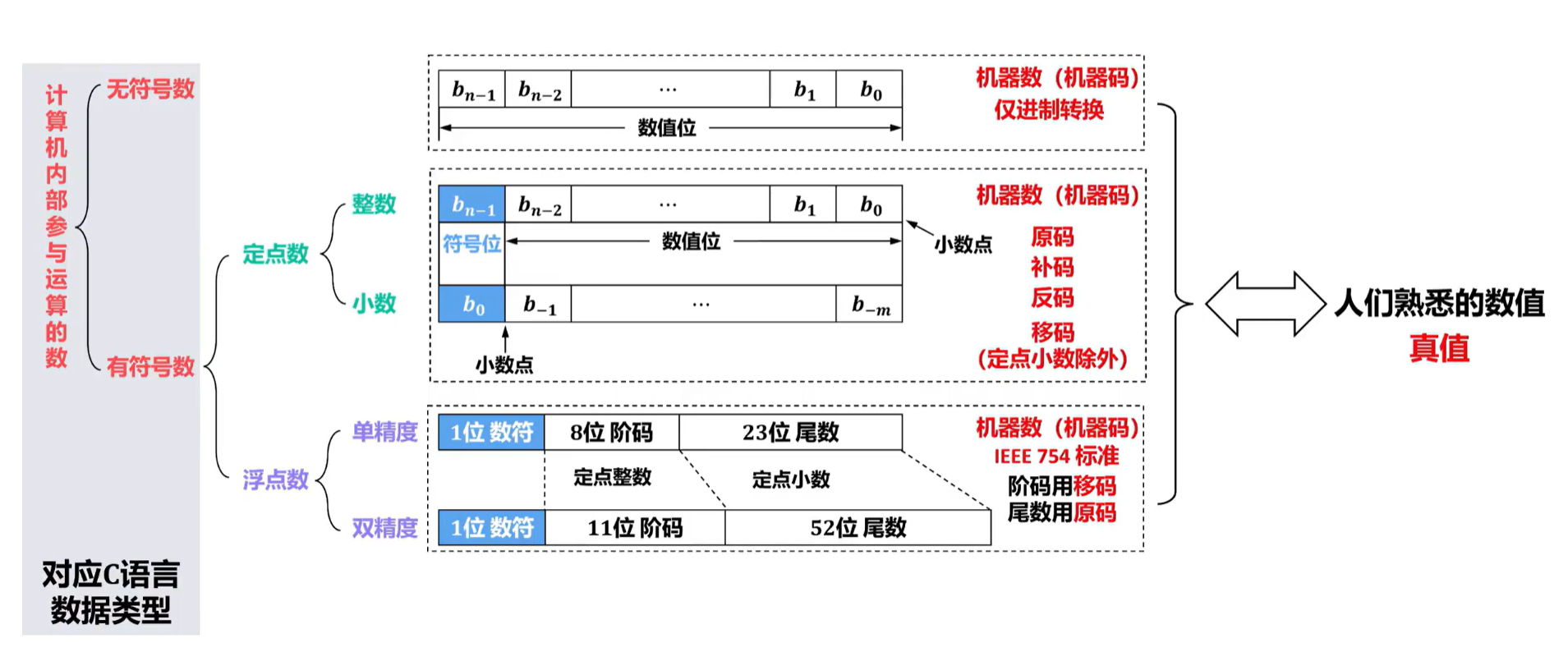
2.1.2 进制转换

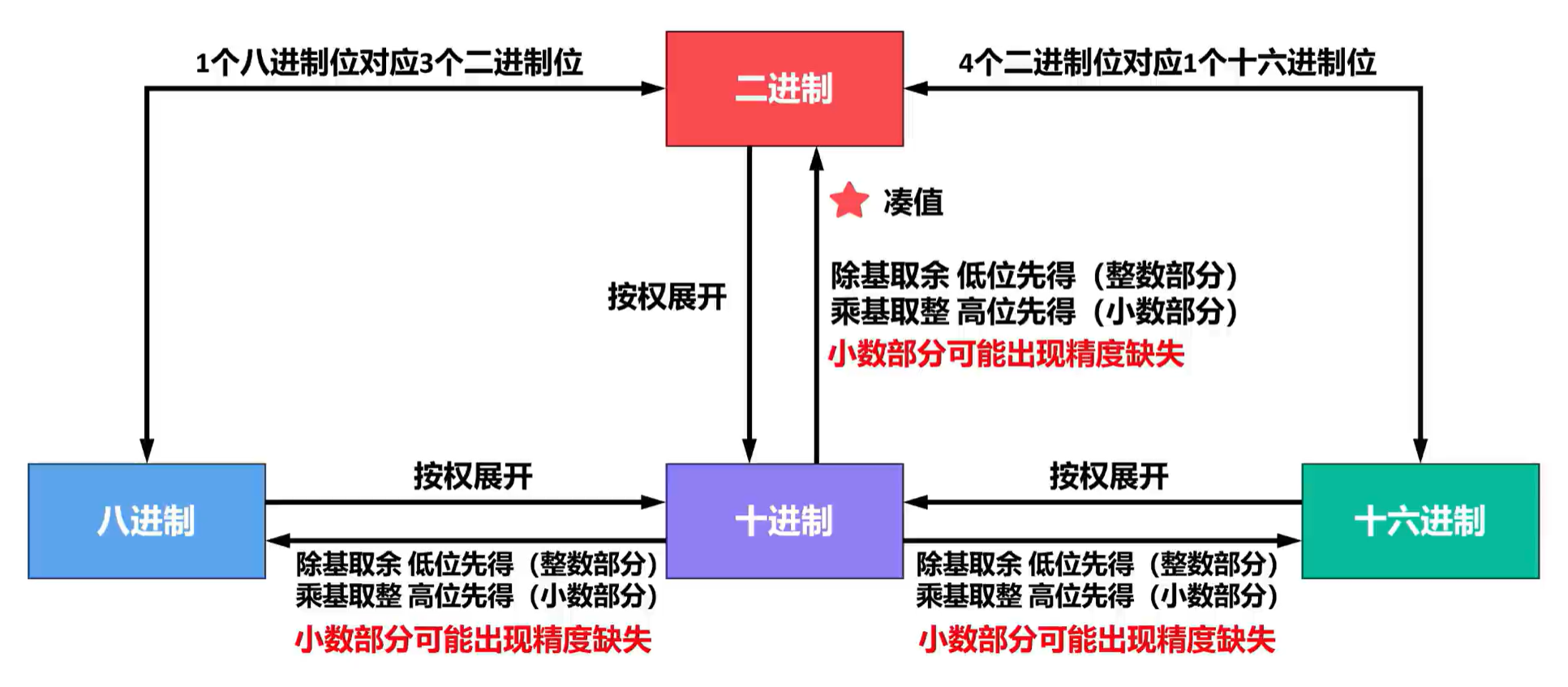
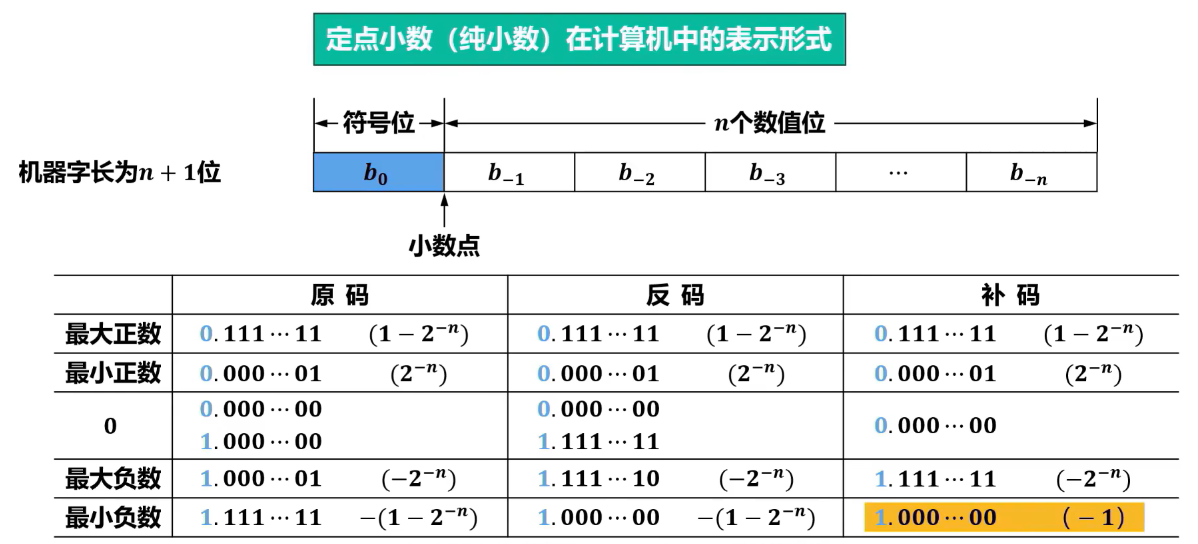
2.1.3 定点数的编码

1.原码

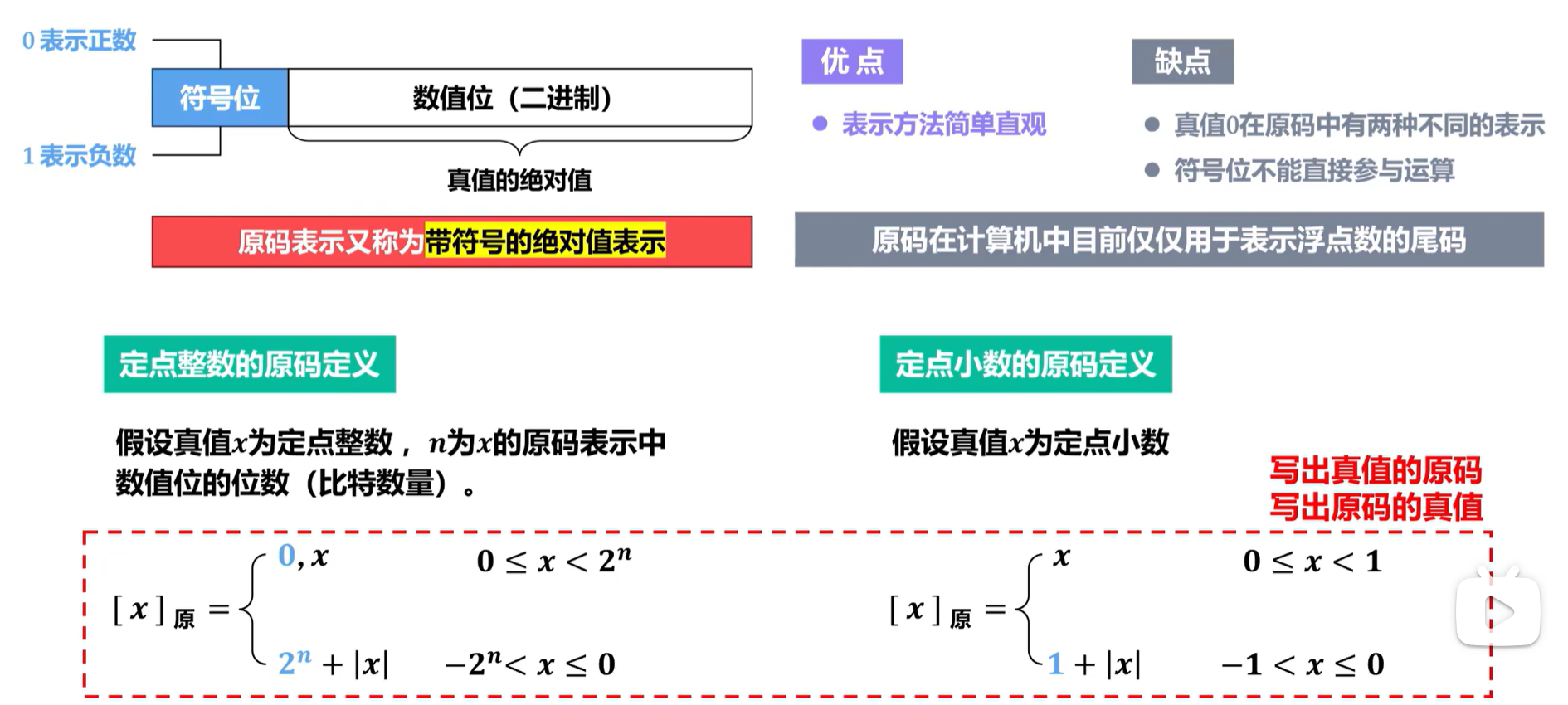
2.补码

原理 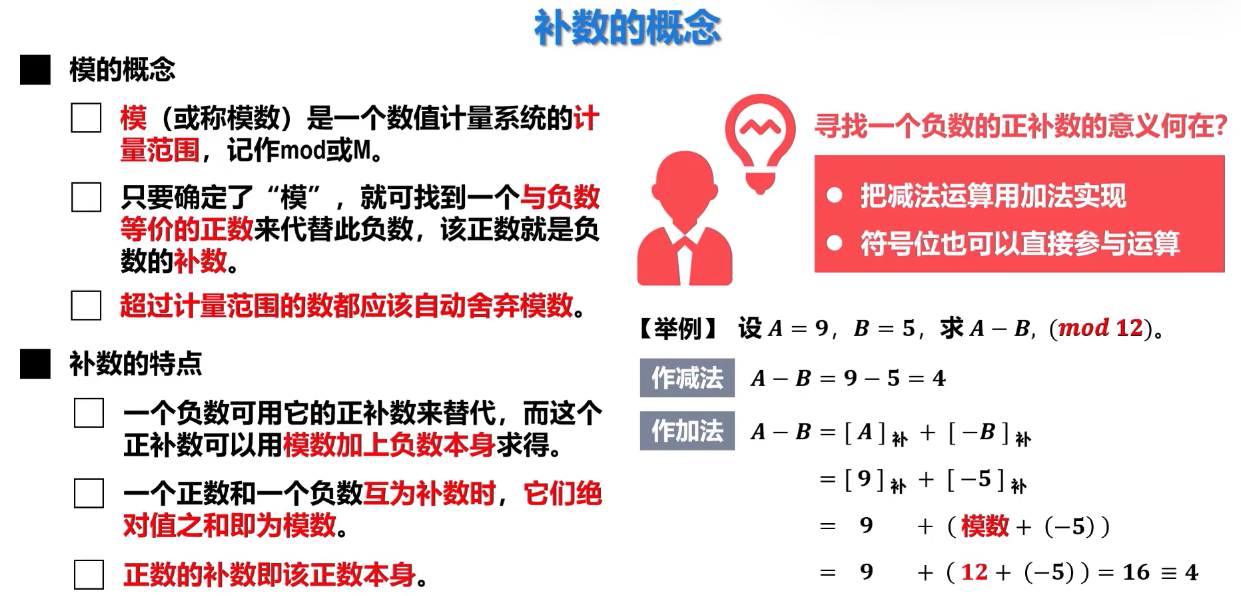定点小数补码的定义

3.反码

反码通常用来作为由原码求补码或者由补码求原码的中间过渡。

• 正数的反码：符号位为 0 ，数值位是它本身。
• 负数的反码：符号位为 1 ，数值位就是真值数值位取反。 定点小数的反码 比较

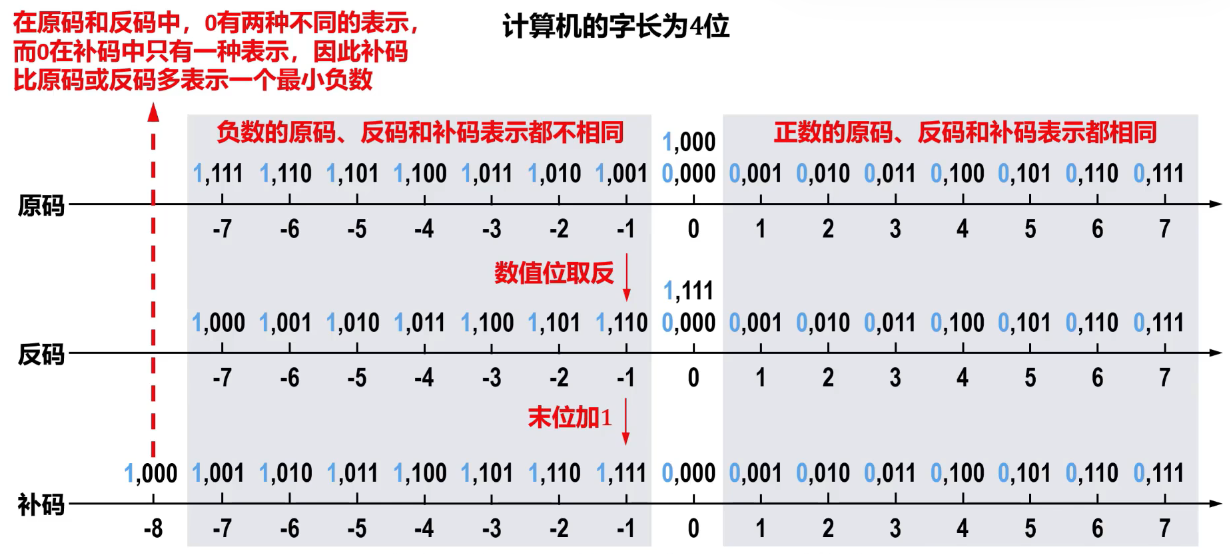
4.移码

移码就是在真值上加一个常数\(2^n\)。

• 在数轴上，移码所表示的范围对应于真值在数轴上的范围向轴的正方向移动 2 个单元。
• 移码只用于定点整数的表示。

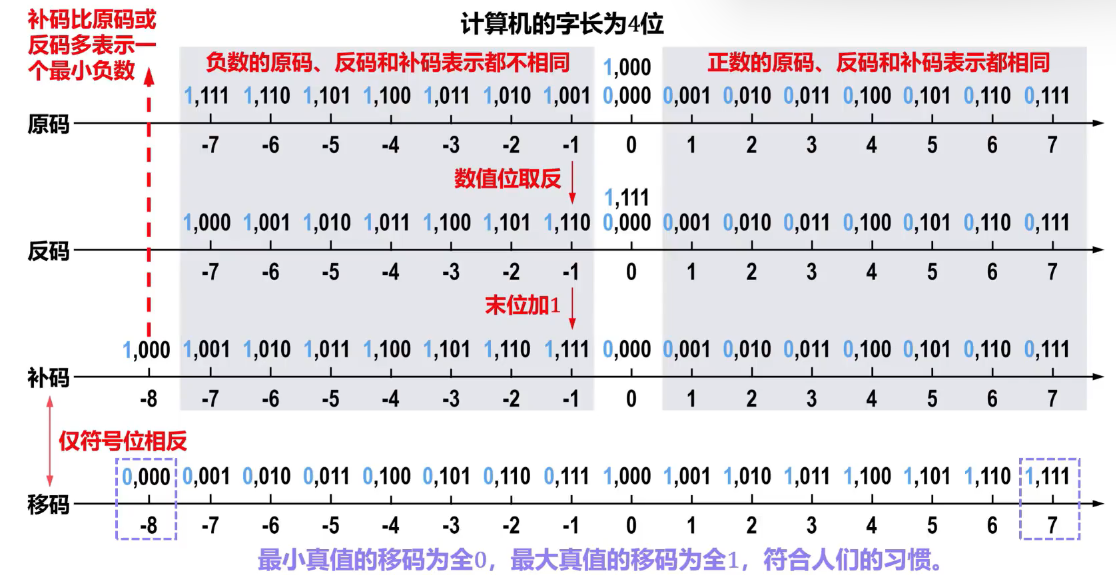
5.相互转换

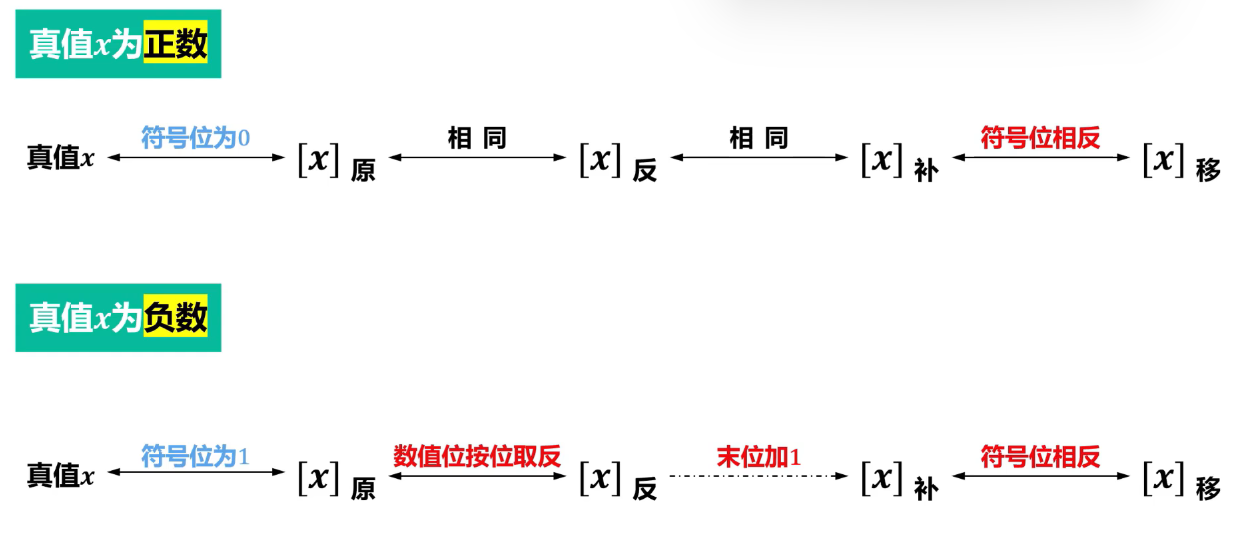
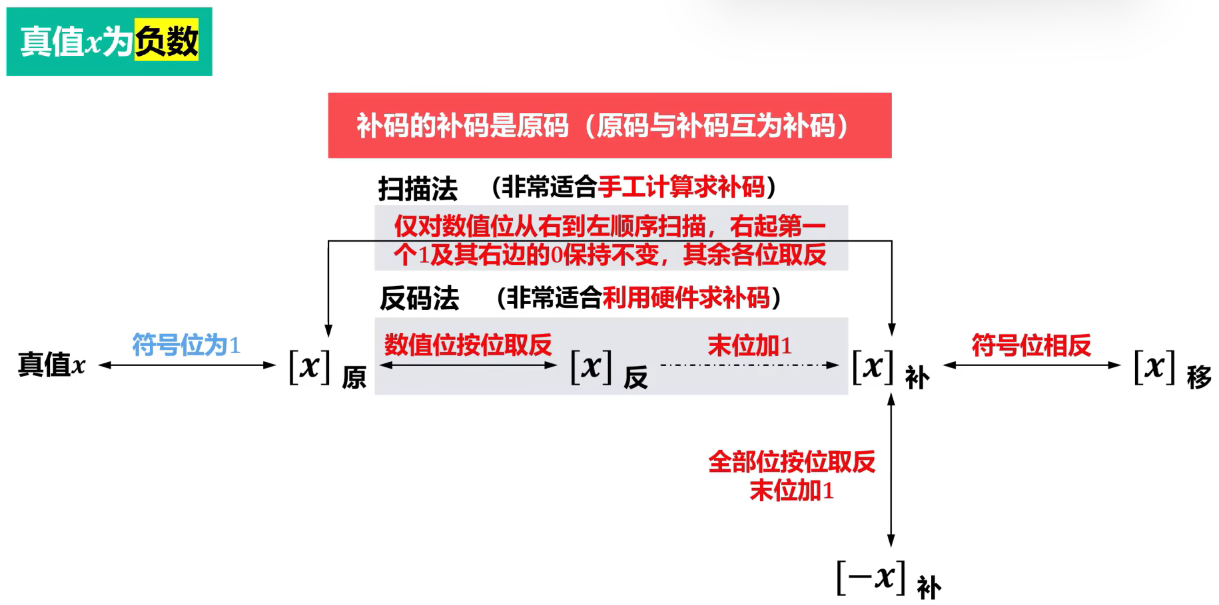易错

2.1.4 浮点数的表示

1.浮点数的表示形式和表示范围

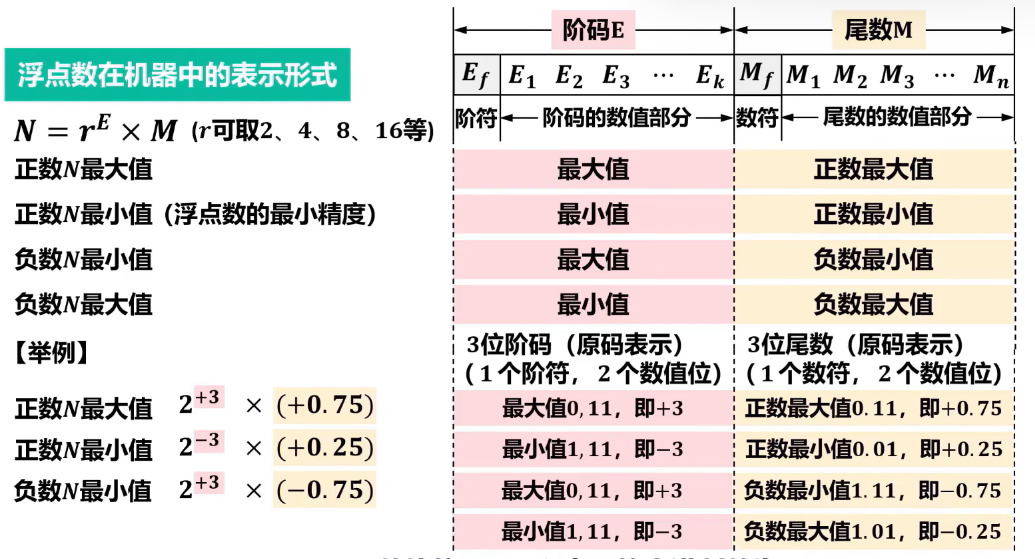就是说，尾数负责决定正负大小，阶码调控倍增。

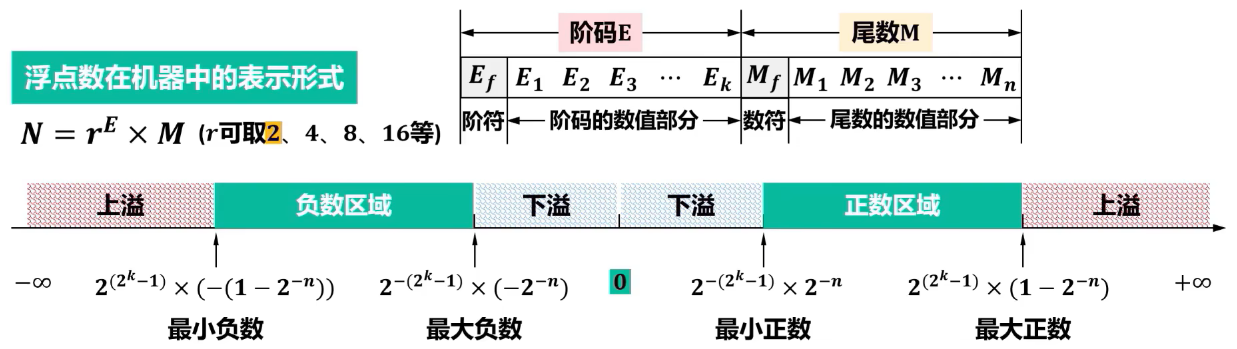
尽管浮点数有效扩大了数据表示范围，但受机器字长限制，浮点数仍然存在溢出现象。

• 当浮点数的阶码大于最大阶码时，称为==上溢==，此时机器==停止运算==，浮点运算器件会显示溢出标志。
• 当浮点数的阶码小于最小阶码时，称为==下溢==，虽然此时数据不能被精确表示，但由于发生下溢时数据的绝对值很小，通常将尾数各位强置为0，按机器0处理，此时机器可以继续运行。
• 当一个浮点数在正、负数区域中但井不在某个数轴刻度上时，也会出现精度溢出的问题，此时只能用近似数表示。 一旦浮点数的位数确定后，合理分配阶码 E 和尾数 M 的位数，直接影响浮点数的==表示范围和精度==。
• 短实数（ 32 位）：阶码 E 取 8 位（含 1 位阶符）尾数 M 取 24 位（含 1 位数符）。
• 长实数（ 6 立）：阶码 E 取 11 位（含 1 位阶符）尾数 M 取 53 位（含 1 位数符）。
• 临时实数（ 80 位）：阶码 E 取 15 位（含 1 位阶符）尾数 M 取 65 位（含 1 位数符）。 （IEEE 754）

1. 阶码的位数决定了数据表示的范围，位数越多，能表示的数据范围就越大。阶码的值决定了小数点的位置。
2. 尾数的位数决定了数据的表示精度。阶码长度相同时，分配给尾数的位数越多，数据表示的精度就越高。

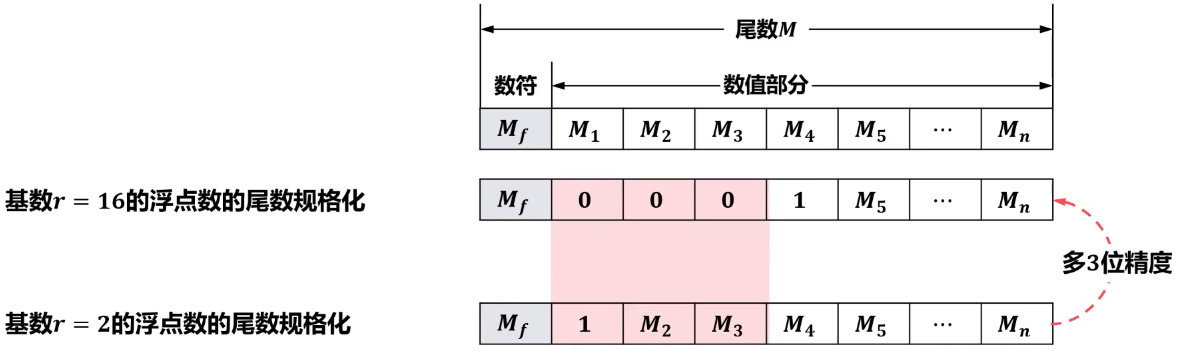
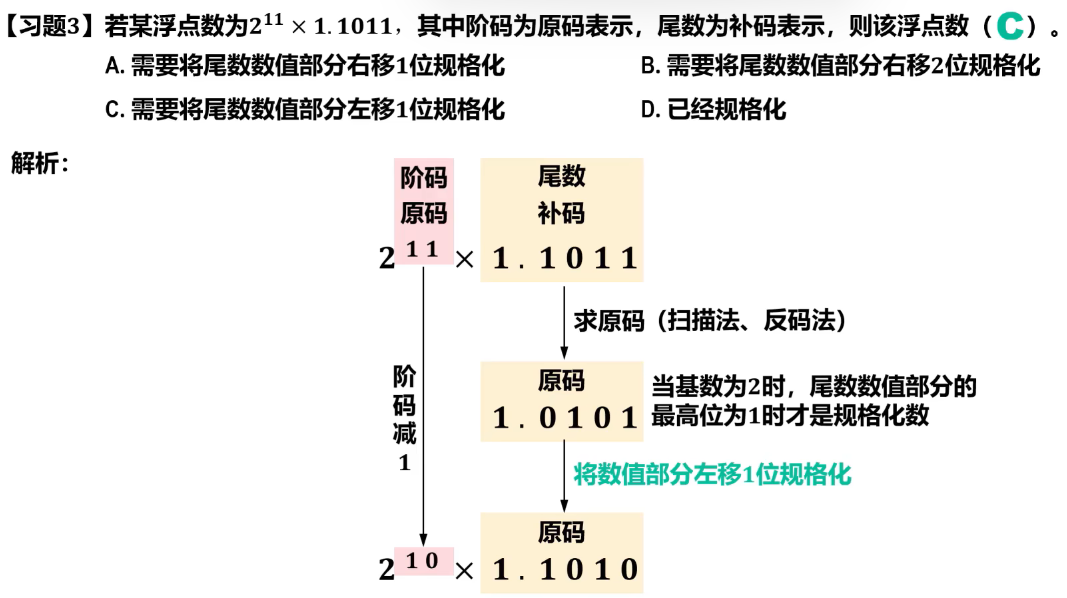
2.浮点数的规格化

• 通常要求浮点数在数据表示时对尾数进行规格化处理即使得尾数的最高数值位必须是一个有效值。从而使得浮点数的表示形式唯一且精度最高。
• 基数 r 不同，对数的表示范围精度等都有影响。一般来说，基数 r 越大，可表示的浮点数范围越大，而且所表示的数的个数越多。但浮点数的精度反而下降。

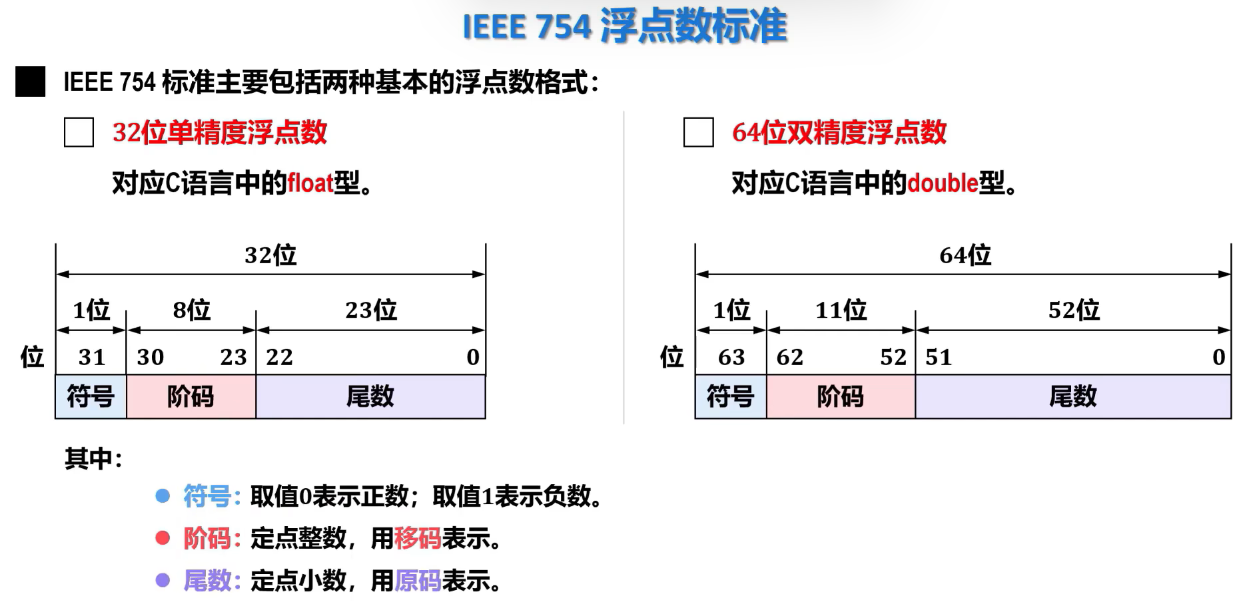
3.IEEE 754浮点数标准

标准概述

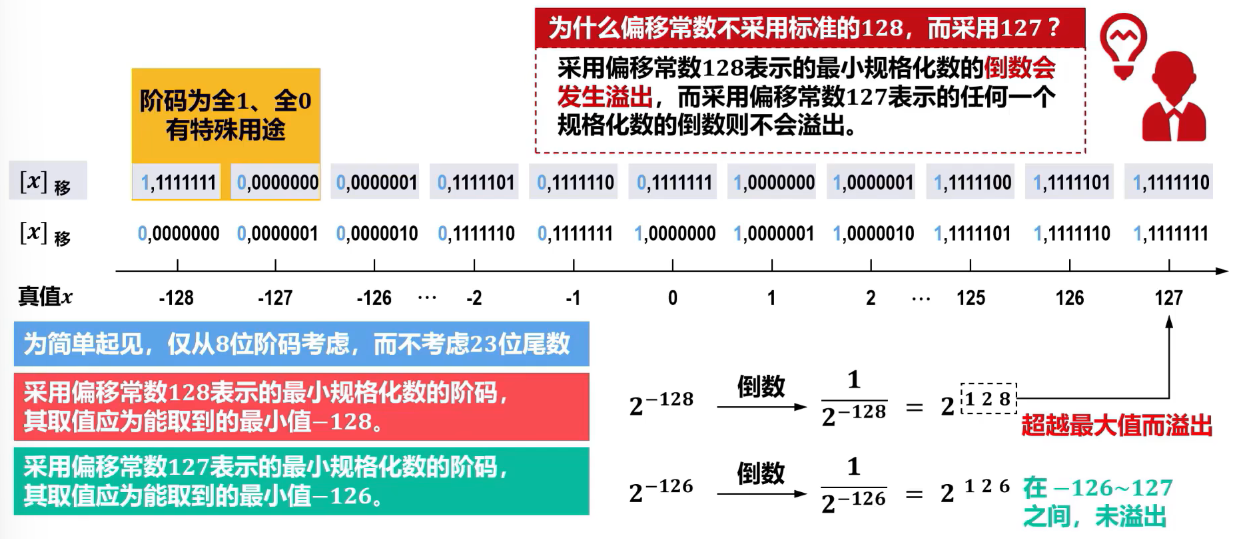
采用移码作为阶码的优点

• 真值 0 在移码中只有一种表示。
• 移码保持了真值原有的大小顺序，可以直接比较大小。
• 最小真值的移码为全 0 ，最大真值的移码为全 1 ，符合人们的习惯。 IEEE 754标准中移码==采用127作为偏移==：

标准细节

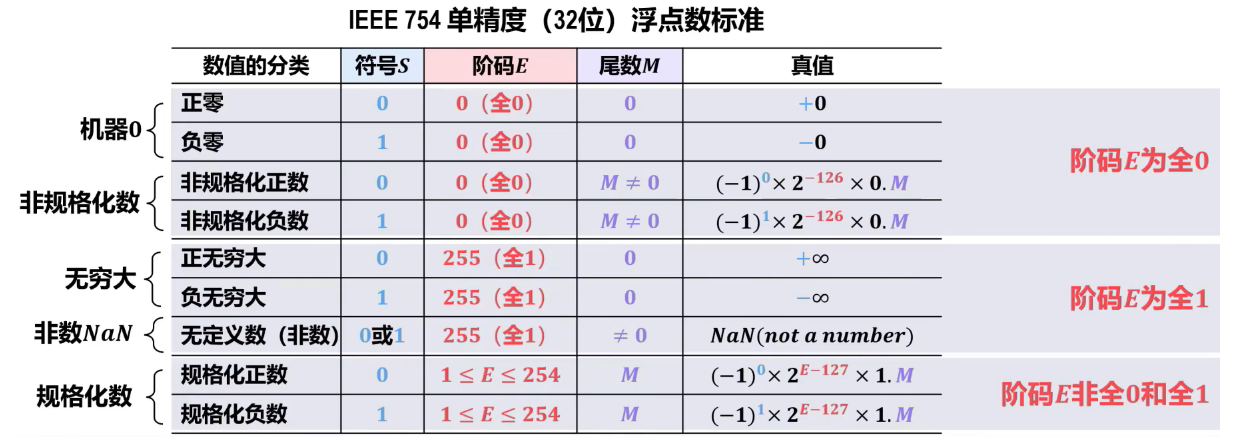注：

1. 一般情况下，-0与+0等效。
2. 引入无穷大数可使计算过程出现异常的情况下程序能继续执行，井且可为程序提供错误检测功能。例如非 0 浮点数除 0 运算的结果就是无穷大，因浮点数除 0 不会像整型赦除 0 一样产生严重错误。
3. 非数 NaN 用于表示0/0、\(\frac{\infty} {\infty}\) 、负数的平方根等。部分非数 NaN 运算结果可能会产生异常。
4. 非规格化数可用于处理阶码下溢，使得出现比最小规格化数还小的数时程序也能继续进行下去。
5. 正常情况下，阶码取==1~254==。

例题

注意符号

单精度浮点数表示范围

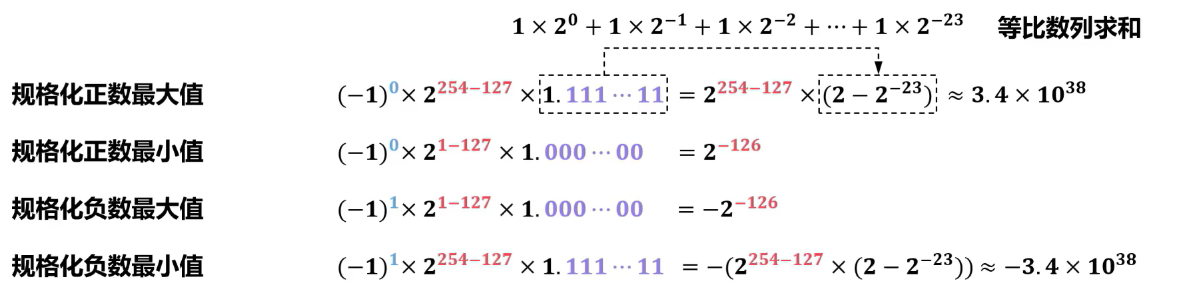
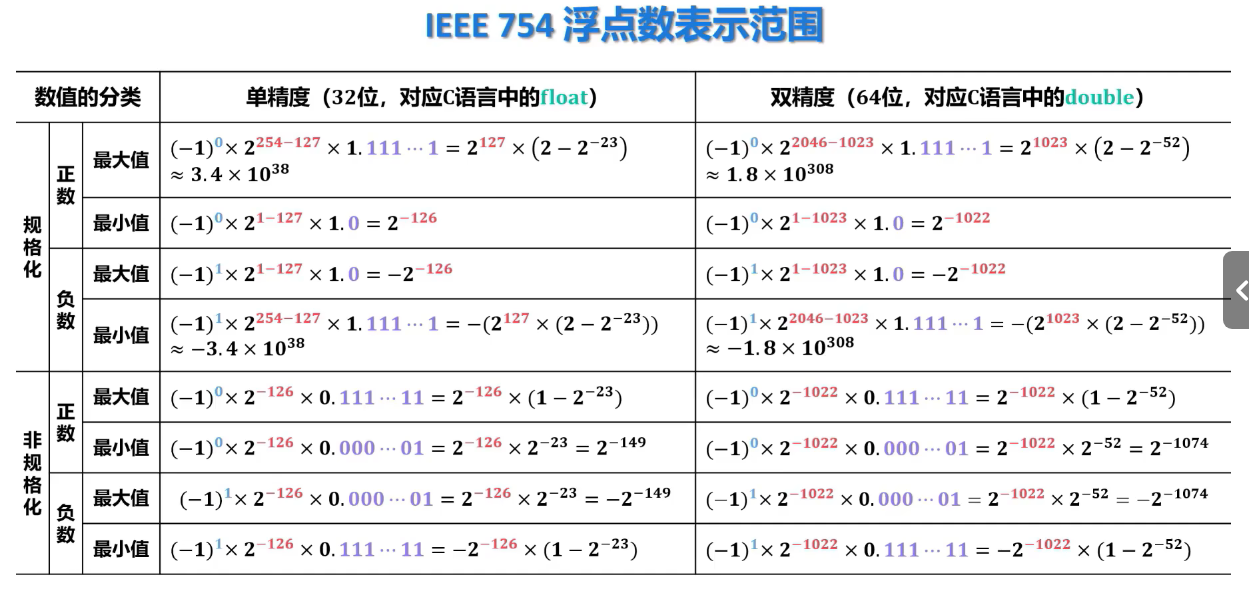
• 十进制小数转换成二进制小数时，可能出现无限循环小数，只能转换到符合精度要求的位数（即所谓的精度缺失）。
• IEEE 754 浮点数格式位数有限（单精度 32 位、双精度 64 位），无法精确表示无限循环小数。通常只能采用舍入的方式近似表示，因此会带来数据表示的误差。这种误差会在计算的过程中不断累积放大，可能导致严重后果。
• 程序员使用二进制浮点数编程时一定要非常小心，要充分考虑浮点数运算可能带来的计算误差，尽量避免对浮点数进行直接比较，在一些对误差极其敏感的情况下，建议采用十进制浮点数进行运算。
• 扩展：

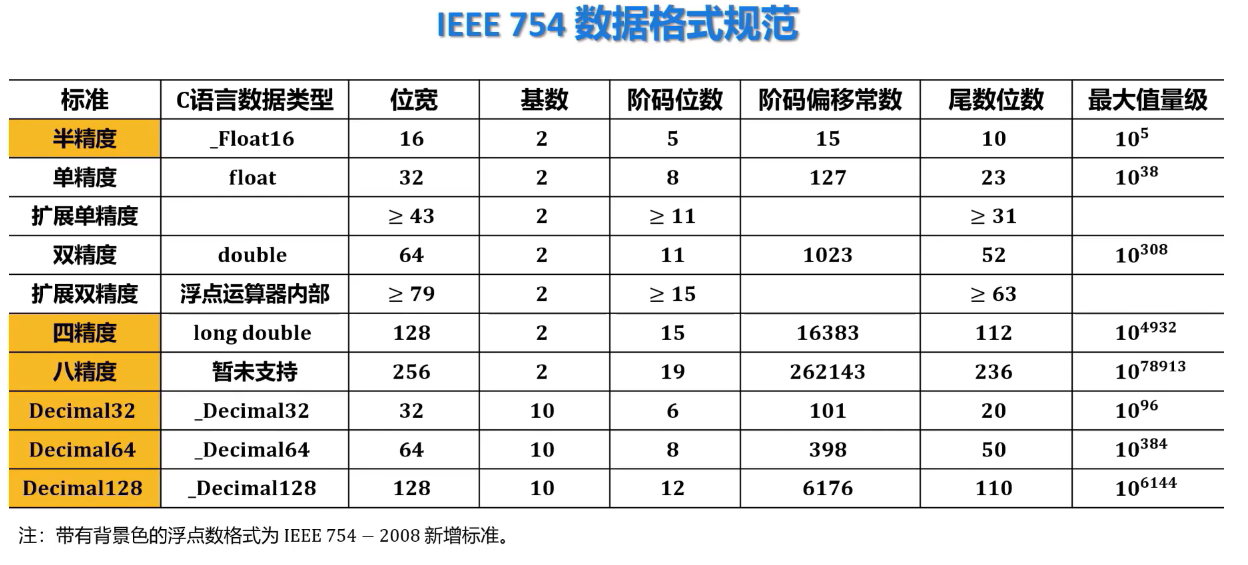
2.1.5 C语言中的数据类型及转换

1.数据类型

• 计算机中的数据以二进制的形式存储在寄存器或存储器中。
• 汇编语言中的数据类型取决于指令操作码。
  • 存储在寄存器、存储器中的操作数本身没有数据类型，对该数进行何种数据类型的操作完全取决于指令。
  • 同一个操作数，既可以当作有符号数，也可以当作无符号数；既可以是定点数，也可以是浮点数。

2.类型转换

整型数据转换

1. 相同字长之间转换：通常是有无符号的转换，保持机器码不变。
2. 小字长转大字长：
   1. 原数据为无符号型：0扩展
   2. ==原数据==为有符号型：符号扩展
   3. 进取决于原数据，与目标类型无关。

char c=-127;
unsigned short us;
us=(unsigned short) c; //11111111 ; 10000001
//us=65409;

3. 大字长转小字长：一般情况下，编译器会将机器码截短处理，表示范围缩小，很可能出错。

short s; unsigned short us ;
char c; unsigned char uc ;
int i
= -40832 ;
s = (short) i ;
us = (unsigned short) i ;
c = (char) i;
uc = (unsigned char) i ;

int、float、double之间的转换

• 上述 3 种类型数据的机器码井不相同（ int 型数据是 32 位有符号整数，用补码表示，分别是 32 位和 64 位浮点数，它们的阶码用移码表示、尾数用原码表示）。
• 上述 3 种类型数据的表示范围精度也不相同。
• 因此在转换过程中编译器只能保证数值尽量相等，大多数情况下只是近似值。

1. float->double：由于 double 型数据的阶码和尾数的位数都比 float 型大，因此其表示范围更大、精度更高，转换后的 double型数据与原 float 型数据的值完全相等。
2. double->float：大数转换：可能发生溢出。高精度数转换：发生舍入。

double a=1234567890123456;
float f=(float)a;
//1234567948140544.000000
double a=1.123456789;
float f=(float)a;
//1.123457

3. float/double->int：小数部分向 0 方向截断，大数转换可能发生溢出。
4. int->float：两种类型都是32位，各自的数据组合数量相同，两者在数轴上表示的数据并不完全重叠。由于 float 型浮点数的尾数包括隐藏位在内共 24 位，当 int 型数据的高 8 位（ 24~31 位）数据为非 0 时，无法精确转换成 24 位浮点数的尾数，此时发生精度溢出。
5. int->double：double 型数据的尾数包含隐藏位在内有 53 位，可以精确表示所有 32 位整数。